Пространственное
и временное
распространение
гравитация
Пауль
Гербер
в
Старгард Померании
Первоисточник
на немецком:
Paul Gerber, Die räumliche und zeitliche Ausbreitung der Gravitation.
Zeitschrift für Mathematik und Physik. 43, 1898, S. 93–104
http://de.wikisource.org/wiki/Die_r%C3%A4umliche_und_zeitliche_Ausbreitung_der_Gravitation
Перевод: Walter Orlov
1. Основной закон
Гравитационные явления демонстрируют собой единственные существующие взаимодействия между отдельными телами, для которых пока не доказанно влияние промежуточного пространства, т.е. наличие от места к месту передаваемого изменения. Тем более понятна надежда, что в конечном счёте однажды удасться получить отсутствующее доказательство. Но не надо рассматривать состояние дел так, как будто эта кажущаяся исключительность не может быть поставленна под сомнение. Все известные и понятые наблюдения склоняют нас в большей мере к противоположному заключению. Отсюда, в случае, если это всё же покоится просто на недостаточном опыте или на не полном анализе, следует сначало показать, что существуют факты, исправляющие и дополняющие наше прежнее представление в противоположную сторону. Поэтому прежде всего необходимо избегать всякую гипотезу, которая предполагает больше, чем то, что в пространстве между двумя гравитационными массами происходит что-то, что имеет отношение к гравитации. Из-за ранних похожих, но всё же не достаточно проработанных трактовок здесь обсуждаемого вопроса следует сослаться на представленный 69-му Собранию исследователей естественных наук реферат о дальнодействии Друде.
Две гравитационные массы дают себя распознать через сопротивление, которые они оказывают увеличению расстояния между ними. С этим должны быть связанны возможные процессы в пространстве между ними, в то время, как они сами могут находиться в покое или в движении. Очевидно с местоположением или с ним и моментальным состоянием движения масс, поскольку исключенны внешние влияния, определяется не только местное сопротивление, но и все следующие до бесконечности сопротивления. Таким образом необходимая для их преодоления работа как и для еденичного сопротивления сама по себе является одной из характеризирующих гравитацию величин. Только она может рассматриваться здесь как основная величина, где важно определить, связанны ли с гравитацией распространяющиеся в постранстве с потерей времени изменения. Ибо по определения нет смысла вести речь о пространственном распространении сопротивления или притяжения, потому что сопротивление и притяжение существуют только в местах, где находятся массы. Но если об одном процессе будет сказанно, что ему требуется время, чтобы попасть от одного места в другое, это значит, что он прекращает существовать в первом месте не оказавшись мгновенно во втором месте; отсюда исчезла бы на некоторое время в процессе содержащаяся энергия, если бы она не проходила через пункты, находящиеся между этими местами. Она равна названной работе, пока процесс относится к гравитации в этих местах расположенных двух масс, потому что тогда он также зависит от их положения и моментального состояния движения, которые не могут объуславливать две различные величины энергии.
Теперь для различия одна масса будет называться притягивающей, другая притягиваемой, под потенциалом V притягивающей массы, действующюю на притягиваемую m, будет пониматься приходящяяся на единицу второй массы часть работы, которую необходимо совершить, чтобы массы удалились друг от друга до бесконечности, которая составляет в общей сложности Vm. Для точки, где находится мысленно закреплённая масса m, и её координат x, y, z относительно также закреплённой притягивающей массы, можно по описанному в Принципах термодинамики Маха расчитать V, поставив ему в соответствие среднее значение в ближайшем окружении точки господствующих потенциалов. V не является направленной величиной и для определённого места в пространстве не меняется со временем. Пусть он в m равен f(x, y, z) и в одной из соседних точек равен
f(x + h, y + h, z + h).
Далее
означает
![]()
вес
соседней
точки в среднем
значении, который
при близкодействии
с растущем
удалением
быстро убывает.
Тогда находим
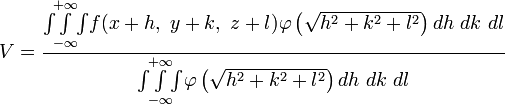
Разложив f в ряд Тэйлора до членов второй степени и интегрируя вокруг точки x, y, z, получим
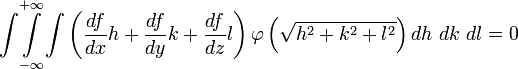
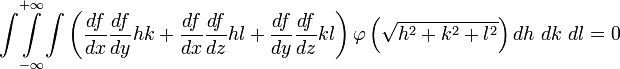
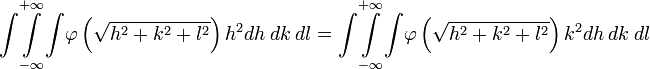
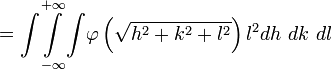
Если
подставить
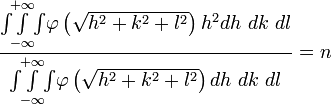
то остаётся
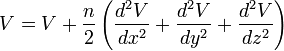
таким образом
Из этого
уравнения
следует известным
образом, если
µ обозначает
константу и
r есть расстояние
между массами
Отсюда
получается
Ньютоновский
закон гравитации.
Потому что V
= µ/r действует
также ещё и в
тот момент,
когда массы
отпускаются.
Прирост Vm
согласуется
с появляющейся
живой силой
dT , и поэтому
в этот момент
T содержит так
же малое
как и V изменение
r во времени.
Следовательно
имеем согласно
общим уравнениям
движения Лагранжа,
посредством
подстановки
на место действующей
на m внешней
силы отрицательную
величину ею
оказываемой
силы, для ускорения
m
Закон
гравитации
Ньютона приписывает
потенциалы,
которые достигают
массы в каждом
положении, если
есть достаточно
времени для
их проявления.
Это условие
всегда исполняется,
пока массы
удерживаютяся
на расстоянии
друг от друга.
Оно нарушается
при возникновении
свободного,
направленного
навстречу друг
к другу движения,
в случае, если
это время имеет
ограниченную
соразмерную
величину. При
этом влияют
два обстоятельства.
Во-первых
именно на расстоянии
![]() между
массами, где
между
массами, где
![]() при
растущем r
положительно,
при уменьшающимся
отрицательно,
потенциал
должен начать
возникать в
обратной пропорции
к
при
растущем r
положительно,
при уменьшающимся
отрицательно,
потенциал
должен начать
возникать в
обратной пропорции
к![]() величине,
потому что
иначе было бы
не понятно, как
это соотношение
могло бы быть
исполненно
при покое масс.
Но он не воздействует
сразу же на m
, потому
что объуславливающий
его процесс
исходит от
притягивающей
массы и требует
время, чтобы
достичь притягиваемую
массу. Само
собой разумеется,
что происходит
движение того
же рода от
притягиваемой
массы к притягивающей
массе, приблизительно
как каждому
тепловому
излучению между
двумя телами
принадлежит
обратное излучение.
Таким образом,
при расстоянии
величине,
потому что
иначе было бы
не понятно, как
это соотношение
могло бы быть
исполненно
при покое масс.
Но он не воздействует
сразу же на m
, потому
что объуславливающий
его процесс
исходит от
притягивающей
массы и требует
время, чтобы
достичь притягиваемую
массу. Само
собой разумеется,
что происходит
движение того
же рода от
притягиваемой
массы к притягивающей
массе, приблизительно
как каждому
тепловому
излучению между
двумя телами
принадлежит
обратное излучение.
Таким образом,
при расстоянии
![]() исходящий
от притягивающей
массы потенциал
исходящий
от притягивающей
массы потенциал
проявится
в m на
![]() позднее
время, после
того как расстояние
стало равным
r .
Во-вторых, при
дальнодействии
потенциал сразу
же проявился
бы в своей полной
величине; однако
в предполагаемом
роде играют
роль пространство
и время, так
требуется
некоторая
продолжительность,
чтобы потенциал,
достигнув m
, передался
этой массе,
т.е. вызвал ему соответствующее
состояние
движения m
.
Потому
что только
принцип дальнодействия
допускает
непостоянство
в явлениях;
замена его
через принцип
близкодействия
имеет прежде
всего целью
зарекомендовавшую
себя в прочих
физических
и химических
изменениях
непрерывность
применить также
в концепции
гравитации.
Отсюда как при
ударе сила
удара складывается
из элементарных
ударов, также
происходит
передача как
потенциал
приходяшего
процесса на
m посредством
следующих друг
за другом
дифференциалпотенциалов.
Если массы
покоятся, движение
потенциала
происходит
с его собственной
скоростью мимо
m ; тогда
переносимая
на m
величина
измеряется
в обратном
соотношении
к расстоянию.
Если массы
сближаются,
уменьшается
время передачи
и с ним передаваемая
величина потенциала
в пропорции
собственная
скорость потенциала
к сумме этой
скорости и
скорости масс,
потому что
потенциал имеет
эту общюю скорость
по отношению
к
m.
позднее
время, после
того как расстояние
стало равным
r .
Во-вторых, при
дальнодействии
потенциал сразу
же проявился
бы в своей полной
величине; однако
в предполагаемом
роде играют
роль пространство
и время, так
требуется
некоторая
продолжительность,
чтобы потенциал,
достигнув m
, передался
этой массе,
т.е. вызвал ему соответствующее
состояние
движения m
.
Потому
что только
принцип дальнодействия
допускает
непостоянство
в явлениях;
замена его
через принцип
близкодействия
имеет прежде
всего целью
зарекомендовавшую
себя в прочих
физических
и химических
изменениях
непрерывность
применить также
в концепции
гравитации.
Отсюда как при
ударе сила
удара складывается
из элементарных
ударов, также
происходит
передача как
потенциал
приходяшего
процесса на
m посредством
следующих друг
за другом
дифференциалпотенциалов.
Если массы
покоятся, движение
потенциала
происходит
с его собственной
скоростью мимо
m ; тогда
переносимая
на m
величина
измеряется
в обратном
соотношении
к расстоянию.
Если массы
сближаются,
уменьшается
время передачи
и с ним передаваемая
величина потенциала
в пропорции
собственная
скорость потенциала
к сумме этой
скорости и
скорости масс,
потому что
потенциал имеет
эту общюю скорость
по отношению
к
m.
Потенциал
движится кроме
как со своей
скоростью c
ещё со скоростью
притягивающей
массы, от которой
он исходит.
Отсюда путь
![]() ,
который проделывают
потенциал и
притягиваемая
масса при встречном
движении за
время
,
который проделывают
потенциал и
притягиваемая
масса при встречном
движении за
время
![]() ,
составляет
,
составляет
где
![]() .
Таким образом
получаем для
расстояния,
с которого
потенциал
начинает возникать,
и которому он
обратно пропорционален,
.
Таким образом
получаем для
расстояния,
с которого
потенциал
начинает возникать,
и которому он
обратно пропорционален,
Потому
что кроме того
скорость, с
которой движения
проходят мимо
друг друга,
имеет величину
потенциал
ввиду временной
задержки своей
передачи на m также пропорционален
Находим
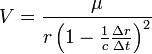
Пока
путь![]() мал
и поэтому
мал
и поэтому![]() мало
по сравнению
с c , можно использовать
dr/dt . В следствии
чего будет
мало
по сравнению
с c , можно использовать
dr/dt . В следствии
чего будет
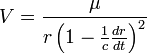
из чего
с помощью ряда
бинома до членов
второй степени
следует
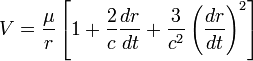
Здесь
в выражении
для V содержится
не только r ,
но также и
производная
r по времени.
Поэтому согласно
общим уравнениям
движения Лагранжа
получаем для
ускорения m
, если dr/dt обозначить
r'
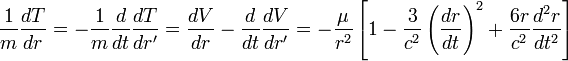
Предположение,
что dr/dt по сравнению
с c мало, исполняется
в области привычных
гравитационных
явлений; иначе
Ньютоновский
закон не оказался
бы верным в той
мере, в которой
он это делает.
Но при особых
условиях, например,
через начальную
скорость, переданной
одной из масс
извне, dr/dt может
стать настолько
большим, что
ему нельзя ни
![]() приравнять,
ни разложение
в биноминальный
ряд до членов
второй степени
не будет больше
достаточным.
Отсюда выведенная
формула годна
только тогда,
если гравитационные
массы представляют
собой свободную
внешне независимую
систему. В этом,
между прочим
важнейшем
случае формула
определяет
изменение,
которое претерпевает
Ньютоновский
закон вследствии
того, что потенциалы
между массами
распространяются
не моментально,
но с потерей
времени.
приравнять,
ни разложение
в биноминальный
ряд до членов
второй степени
не будет больше
достаточным.
Отсюда выведенная
формула годна
только тогда,
если гравитационные
массы представляют
собой свободную
внешне независимую
систему. В этом,
между прочим
важнейшем
случае формула
определяет
изменение,
которое претерпевает
Ньютоновский
закон вследствии
того, что потенциалы
между массами
распространяются
не моментально,
но с потерей
времени.
2. Скорость распространения
В зависимости от того, дают ли наблюдения для введённой в предыдущем расчете величины c конечно или бесконечно большую величину, с большей или меньшей определённостью находим, что потенциалам гравитационных масс требуется время, чтобы преодолеть расстояния между ними, или что такое временное распространение не существует и таким образом гравитация покоится на реальном дальнодействии. Особо требуется исполнение двух условий. Во-первых, из-за перевеса c над dr/dt члены выражения для ускорения массы m, содержащие c, отделить от общего выражения и сделать их сравнимыми с фактами; во-вторых, определить порядок, через который распознавалось бы существование конечной величины c, и после этого сверить с опытом. Так как место действия фактов может быть только планетная система, будем представлять себе в качестве притягивающей массы Солнце и притягиваемой одну из планет. Для простоты движение последней будет рассматриваться по отношению к Солнцу как к начальной точки, так что постоянная µ в соотношении суммы масс будет выглядеть увеличенной для притягиваемой массы.
Положим
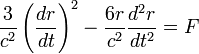
Таким образом
из
чего посредством
умножения
одного уравнения
на y и
другого на x
и через вычитание
следует
Это
уравнение
получается
также при выводе
параметров
и орбиты планетарного
движения из
Ньютоновского
закона, которое
через интегрирование
и введение
полярных координат,
где![]() есть
угол между
радиусвектором
и позитивной
осью абцисс
и L означает
константу,
приводит к
есть
угол между
радиусвектором
и позитивной
осью абцисс
и L означает
константу,
приводит к
Подставим в этом содержащююся величину
![]()
а также
в
уравнения для
тогда
они будут выглядить
С
константами
M
и N получим
путем интегрирования
Так как
находим из обоих уравнений
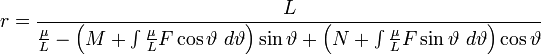
Интегралы
в знаменателе
принимают раз
за разом другие
и другие значения,
в случае, если
F не исчезает.
Заранее предположив,
что известно
её значение
к определённому
времени, тогда
можно сказать,
что планета
к этому времени
находится на
через описываемым
этим уравнением
эллипсе. Являются
его большая
полуось a,
малая полуось
b, числовой
эксцентриситет![]() и
угол между a
и позитивной
осью абцисс
и
угол между a
и позитивной
осью абцисс![]() ,
и разрешив
уравнения для
,
и разрешив
уравнения для
![]() и
и ![]()
![]() и
и ![]()
![]()
![]()
Видно,
если учесть
неизменность
![]() ,
что движение
планеты допускает
такую интерпритацию,
как если бы она
двигалась бы
по эллипсу,
чьи
,
что движение
планеты допускает
такую интерпритацию,
как если бы она
двигалась бы
по эллипсу,
чьи![]() и
и![]() постоянно
меняются. Только
для случая F
= 0 прекращается
это изменение.
Значит оно есть
то, отчего наличие
конечной величины
c проявляется
в действии.
После дифференцирования
последних двух
уравнений по
постоянно
меняются. Только
для случая F
= 0 прекращается
это изменение.
Значит оно есть
то, отчего наличие
конечной величины
c проявляется
в действии.
После дифференцирования
последних двух
уравнений по![]() ,
подстановки
выражения для
L , и поделив
одно уравнение
через
,
подстановки
выражения для
L , и поделив
одно уравнение
через
![]()
![]()
![]()
Через
приравнивание
обоих выражений
получится с подстановкой![]()
из чего в обратном порядке
Чтобы
посредством
этой величины
получить содержащее
наблюдаемые
величины уравнение
для ![]() ,
представим F как
производную
r по
t. Имеем,
опять же с учётом
неизменности
,
представим F как
производную
r по
t. Имеем,
опять же с учётом
неизменности![]() и
кроме того с
использованием
формул
и
кроме того с
использованием
формул
![]()
![]() и
и ![]()
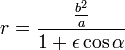
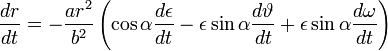
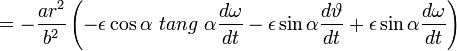
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом
Отсюда
искомое уравнение
для![]()
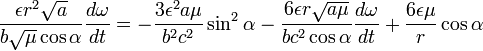
или после подстановки
![]() и
и ![]()
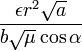
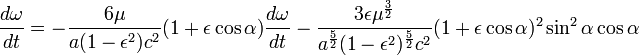
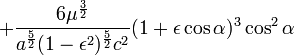
Если
мы желаем таким
образом полученное
значение
скорости![]() сравнить
с наблюдениями,
следует учесть,
что расчёт
возможен только
для единственной
планеты. Отсюда
попадают под
рассмотрение
лишь те движения
перигелия,
которые возникают
не вследствии
возмущений.
Такие известны
только у Меркурия
с общей суммой
примерно 41"
в столетие. Эта
незначительность
заранее исключает
любое эмпирическое
определение
непрерывности
изменения
сравнить
с наблюдениями,
следует учесть,
что расчёт
возможен только
для единственной
планеты. Отсюда
попадают под
рассмотрение
лишь те движения
перигелия,
которые возникают
не вследствии
возмущений.
Такие известны
только у Меркурия
с общей суммой
примерно 41"
в столетие. Эта
незначительность
заранее исключает
любое эмпирическое
определение
непрерывности
изменения![]() . Таким образом
следует интегрировать
через большой
промежуток
времени. В последнем
уравнении
встречается
только
. Таким образом
следует интегрировать
через большой
промежуток
времени. В последнем
уравнении
встречается
только![]() без
без![]() ;
где изменение
;
где изменение
![]() по
сравнению с
самой
по
сравнению с
самой![]() исчезающе
мало, так что
можно рассматривать
последнюю как
постоянную.
После этого
достаточно
выбрать в качестве
границ интегрирования
исчезающе
мало, так что
можно рассматривать
последнюю как
постоянную.
После этого
достаточно
выбрать в качестве
границ интегрирования
![]() и
и![]() ,
потому что
,
потому что![]() при
каждом последующем
обороте приблизительно
повторяет значения предыдущего
обращения.
при
каждом последующем
обороте приблизительно
повторяет значения предыдущего
обращения.
Уравнение
для![]() умножим
на
умножим
на![]() и
подставим во
второй и третий
член правой
стороны
и
подставим во
второй и третий
член правой
стороны
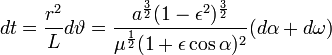
Посредством подходящего упорядочения и деления получается
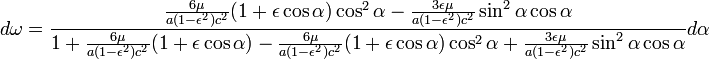
Поделив числитель и знаменатель на
расставив
слагаемые по
растущей степени
![]() и
использовав
сокращение
и
использовав
сокращение
![]()
уравнение станет
Приближенно получим
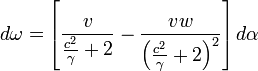
Для
движения перигелия![]() в
течении одного
оборота получается
в
течении одного
оборота получается
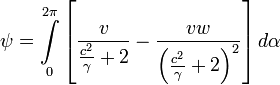
или, потому что
![]()
![]()
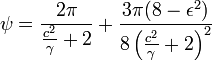
Отсюда следует
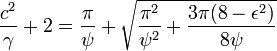
Учитывая,
что![]() очень
мало, видно,
что второй член
под корнем по
сравнению с
первым исчезнет.
Итак будет
очень
мало, видно,
что второй член
под корнем по
сравнению с
первым исчезнет.
Итак будет
![]()
где
по той же причине
![]() в сравнении
с
в сравнении
с![]() может
не учитываться.
В конечном
счёте получаем
может
не учитываться.
В конечном
счёте получаем
Здесь
где![]() означает
период обращения
планеты. Специально
для Меркурия
имеем следующие
величины:
означает
период обращения
планеты. Специально
для Меркурия
имеем следующие
величины:
![]() км,
км,
![]() ,
,
![]() дней,
дней,
![]() .
.
![]() км/с.
км/с.
Меньшую до сих пор полученную скорость света получил Фуко - равна 298000 км/с; наибольшая получается по методу Рёмера из новейших наблюдений 308000 км/с; Герц в своих опытах нашёл скорость электромагнитных волн 320000 км/с. Таким образом скорость, с которой распространяется гравитационный потенциал, соответствует скорости света и электромагнитных волн. Одновременно в этом заключенна гарантия, что эта скорость существует.
Конечно никто не будет отрицать, что смещение перигелия Меркурия на 41" в столетие также может быть объусловленно через другие ещё не известные обстоятельства, так что не существовало бы необходимости в конечной скорости гравитационного потенциала. Но если учесть, что здесь в основном решающяя, между прочим также описывающяя отклонение всех предыдущих результатов похожих исследований формула для зависимости потенциала от такого рода скорости получена совершенно естественным путём без какого-либо использования тяжёловесных гипотез. Поэтому это было бы особой случайностью, если бы 41 секунд Меркурия прямо приводила к световой и электрической скорости, не имея ничего общего с пространственновременным распространением гравитации, потому что всё же медиум, в котором происходит это распространение и движение света и электрических волн, есть тот же, что и в пространстве между космическими телами. Даже относительно большое движение перигелия, которое получается с найденным значением c для Венеры, а именно 8" в столетие, не может являться безупречречным возражением; или ревизия возмущений этой планеты должна окончательно исключить возможность этого числа. Необходимо также напомнить, что расчеты векового ускорения Луны могли бы колебаться между 6" и 12". В остальном получаются сплошь незаметно малые движения перигелия. Они составляют согласно полученным из используемых таблиц наблюдаемых величин для Земли в столетие 3",6, для Луны 0",06, для Марса 1",3, для Юпитера 0",06, для Сатурна 0",01, для Урана 0",002 и для Нептуна 0",0007.